近年、年齢ごとの標準値などを考える際に、LMS法という統計手法が用いられることが多くなっています。

従来の正規分布の考えと、その考え方からなぜLMS法が生まれてきたかを解説します。

正規分布とは？

まず、LMSについて考える前に、正規分布(normal distribution)についておさらいしましょう。

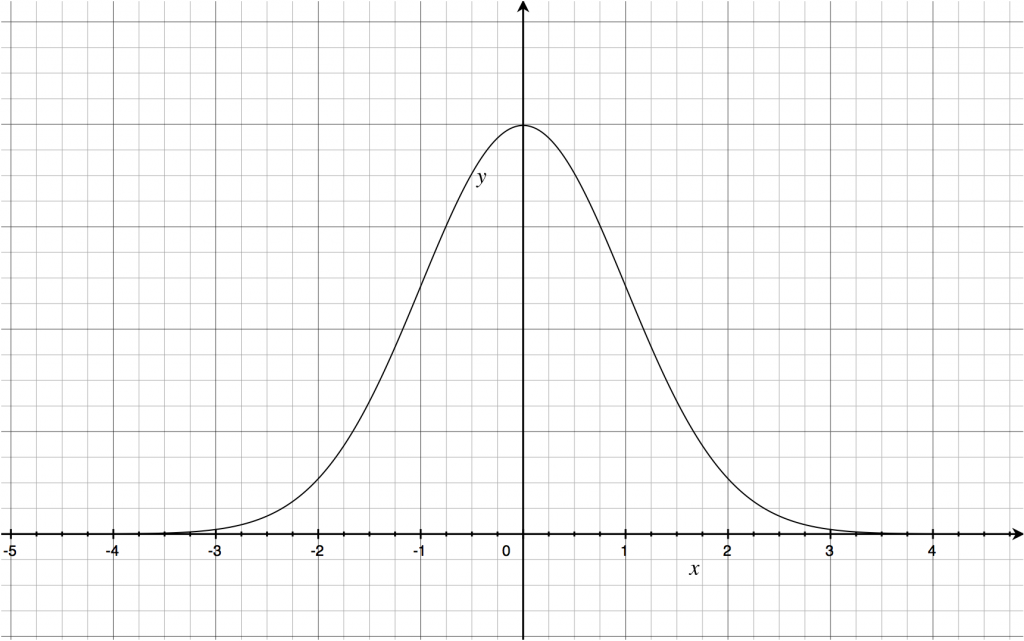
正規分布とは平均を中心とした左右対称山形の確率分布です。

よく、高校数学や統計学の教科書で下のようなグラフを眼にしたことがあると思います。

中央に行くほど山が高くて、裾野に行くほど左右対称に低くなっています。

この正規分布は統計学において頻繁に利用されており、多くの統計的手法(t検定や分散分析など)が、母集団が正規分布に従っていると仮定して使用されています。

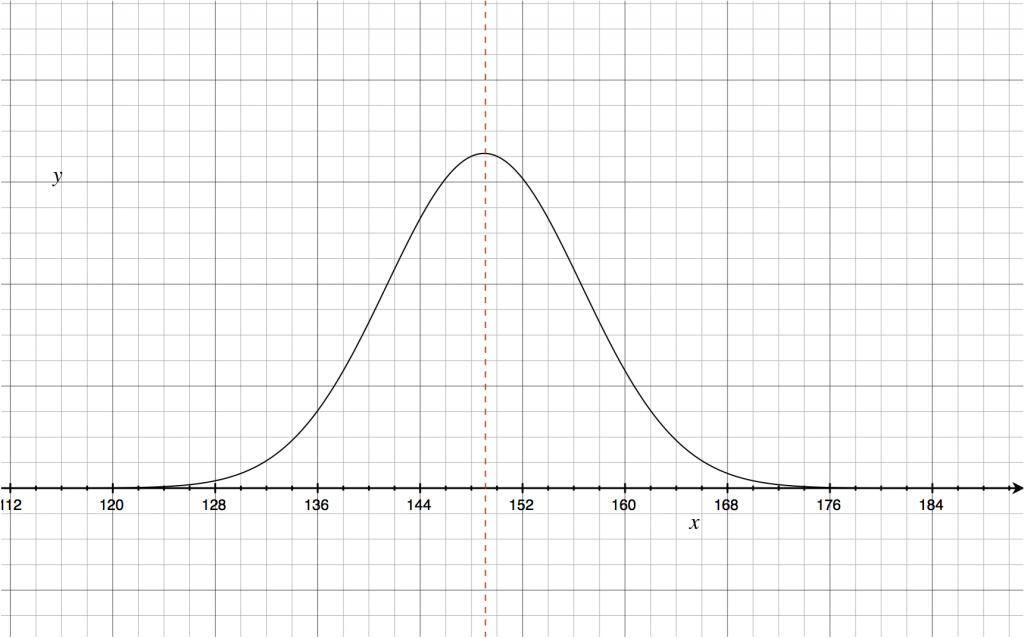
たとえば、12歳の男児の身長を考えてみましょう。平均149.1[cm], 偏差 7.6 [cm] で下のようなグラフで表せます。

赤い線が平均(149.1[cm])です。このグラフを見れば

• 12歳の男児では、149[cm]付近の子が多いこと。
• 140[cm]くらいの子と160[cm]くらいの子は同じくらいの人数がいること。
• 165[cm]を超える子は割合としてはかなり少ないということ。

がわかります。

また、平均からどのくらい離れているかをZスコア(SDスコア)を用いることで表すことができます。例えば、身長 156.7[cm]の子は、平均からちょうど偏差分だけ離れている(156.7 - 149.1 = 7.6)ので+1.0 SDと表すことができます。これによって同じ年令の子どもと比べてその子の身長がどうか、また背の低かった子は、2年前と比べて身長が他の子に追いついてきているのかそれとも離れていっているかを簡単に調べることが出来るようになりました。

LMS法とは？

大変便利な正規分布ですが欠点がありました。それは、表したい数値が正規分布に従っていない場合には使用できないというところです。

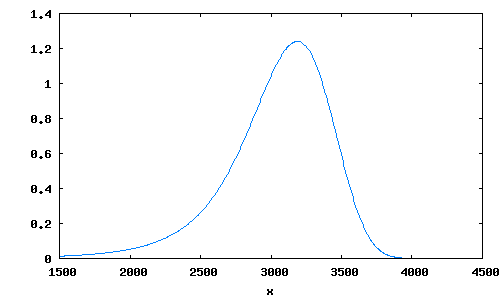
たとえば、予定日ちょうどで生まれた男児の体重は下のグラフのようになっています。

(注: 実際は下記ほど偏り方(歪度)が強くないです。説明をわかりやすくするために少し誇張して描いています。)

出生体重は上のように正規分布に従っておらず、山が少し右に偏っていて、裾野が左に長い形をしています。

このように表したい数値が正規分布に従っていない場合に、Box-Cox変換を行うことで正規分布に近づけることがあります。

LMS法は、従来の平均(LMSのMに相当)と正規分布の幅の広がり方(LMSのSに相当)に加え、Box-Cox変換の係数であるL(歪度)を加えることで左右に偏ったデータを表せるように拡張したものとなっています。